A Novel Equation Correlating the Rheological Properties of Some Commercial Tomato Ketchups
I. Stanciu*, A. Messaâdi, O. Díez-Sales, S.S. Al-Jameel, E. Mliki, J.V. Herráez, N. Ouerfelli
Abstract
This article is focused on evaluating the rheological properties of tomato ketchup. The purpose of the paper was to show the importance of knowledge about the rheological properties of ketchup and to find new more adequate equations of the temperature-viscosity dependence. All measurements were performed under the same temperature conditions at approximately 25 °C and shear velocities between 5.46 and 700.41 s-1. Ketchup is a non-Newtonian material, so the apparent viscosity was measured.
We found out that the apparent viscosity decreased exponentially with increasing temperature, so the Arrhenius equation is valid. Ketchup fluidity increases exponentially with temperature, which leads us to propose an original logarithmic expression correlating the shear stress and the square root of shear rate with only two adjustable parameters with some physical significance. The model is compared with some previous ones showing that the calculated rheological characteristics can be used to design the technological equipment or containers for the distribution of the product to the end-users. A comparison between parameter values of different fluids can contribute to the knowledge of the flow behavior is also important for the development of new recipes and the direct qualitative evaluation of the products.
Keywords: Tomato ketchup, Modeling, Pseudoplastic, Viscosity, Power-law, Rheology, Correlation.
Introduction
Tomatoes are consumed worldwide, and represent an important part of the human diet and a rich source of b-carotene, folates (vitamin B9), potassium, vitamin C, vitamin E, flavonoids, and lycopene (Fakirabad & Abedi, 2019). Tomatoes can be consumed fresh, but important quantities are processed to obtain different products, including tomato juice, paste, puree, ketchup, and sauces (Bourne, 2002; Sahin & Ozdemir, 2004; Fortuna et. al., 2004; Śmigielska et. al., 2013).
To meet consumers' quality requirements, some quality parameters of tomato sauce-based products are to be considered very important, such as rheological and appearance indicators (i.e. consistency and color). It was reported that tomato-based products characterized by high viscosity and red color are preferred by consumers (Bourne, 2002; Sahin & Ozdemir, 2004; Fortuna et. al., 2004; Śmigielska et. al., 2013).
Different ingredients (e.g. additives) are allowed to be included in tomato sauce and have been reported to affect multiple properties of tomato sauce. Long-chain polymers, such as hydrocolloids (polysaccharides and proteins), are extensively used by the food industry in different systems as soups, beverages, desserts, ketchups, sauces, or salad dressings, due to their functionality as thickening (Bourne, 2002; Sahin & Ozdemir, 2004; Fortuna et. al., 2004; Śmigielska et. al., 2013).
This study aims to explore and model the effect of different ingredients on commercial textured tomato ketchup with modified regular corn starch in terms of rheological properties.
The knowledge of the physical qualities of food materials is necessary in the processes controlled in their manufacture, operation, and handling. In order to determine the quality of food materials, it is important to know the physical properties such as mechanical, thermal (Kubík Ľ et. al., 2014; Kubík Ľ et. al., 2017; Dizayee & Maaroof, 2019), thermo physical (Božiková et. al., 2010; Glicerina et. al., 2013; Micić et. al., 2014; Hailu et al., 2018), and rheological (Glicerina et. al., 2013; Hlaváč et. al., 2012; Bikić et. al., 2012; Bukurov et. al., 2012; Diósi et. al., 2014).
Tomatoes can often be eaten fresh, but there are several varieties that are processed into various products, such as tomato sauce, soup, pasta, puree, juice, ketchup, and salsa (Tan et.al. 2015). Some researchers have investigated the benefits of tomatoes in reducing the risk of heart disease, improving bone health, and lowering the risk of cancer (Tan et.al., 2015; Alexandrovich et al., 2018). Through the industrial processing of tomatoes, they lead to a great variety of products. The most relevant products are as follows: concentrated tomato products, either in the form of puree or paste, depending on the percentage of natural soluble solids; pizza sauce, made from shells and seeds; tomato powder, in the form of dehydrated concentrated tomatoes; tomatoes peeled, whole or cut into cubes; ketchup, tomato sauce seasoned with vinegar, sugar, salt and a few spices, etc. (Ruiz et. al., 2009). Studies of changes in tomato powder during storage at different storage temperatures have been evaluated for five months by (Liu et. al., 2010). Some researchers have found that higher storage temperatures have a significant effect on the qualities of tomato puree, while lower temperatures had a smaller effect. Tomato puree has many benefits, including ease of packing, transport, and mixing. In addition, tomato puree can be used as an ingredient in many foods, mainly soups, sauces, and ketchup (Liu et. al., 2010).
The rheological properties of tomato products are considered as one of the most important quality attributes because they influence the processing parameters of the products, in particular, the flow properties during transport, as well as the acceptability of consumers (Torbica et. al., 2016). Investigation of the rheological properties and microstructure of tomato puree using continuous high-pressure homogenization was performed (Tan et. al., 2015). The influence of the rheological and structural characterization of tomato paste on the quality of ketchup has been investigated by (Bayod et. al., 2008). According to (Sharoba et. al., 2005), ketchup is a non-Newtonian, semi-solid, time-independent liquid with a defined shear rate. The effect of temperature on fluid viscosity at a specified shear rate could be described by the Arrhenius equation, where the apparent viscosity decreases as an exponential function with temperature (Sharoba et. al., 2005). According to (Bayod et. al., 2008), the viscosity of tomato ketchup is a major quality component for consumer acceptance. Some parameters affect the flow behavior of tomato ketchup, including the quality of the raw material (eg tomato paste) and the processing conditions. In order to obtain a constant and desirable quality in the final product (i.e. ketchup), a high-quality paste is required and continuous control and adjustment of the variables for its processing (Bayod et. al., 2008). Tomato ketchup could be presented as a concentrated dispersion of insoluble matter in aqueous media, and its complex structure determines that it exhibits a non-Newtonian, thin shear, and time-dependent rheological behavior (Torbica et. al., 2016). Ketchup can be included in one of the most consumed spices, obtained from either fresh or concentrated tomatoes, such as tomato puree and tomato paste (Mert, 2012). Concentrated tomato paste is usually stored and used as an intermediate with water and other ingredients to be reconstituted into end products such as ketchups and sauces (Zhang et. al., 2014).
The effect of temperature and concentration on the rheological properties of ketchup processed cheese mixtures was analyzed using a constant and dynamic oscillatory shear by (Yilmaz et. al., 2011). The temperature dependence of the apparent viscosity at a specified shear rate (50 s-1) could be described by the Arrhenius model (Yilmaz et. al., 2011). Some researchers have analyzed linear creep and recovery of ketchup processed cheese mixtures using mechanical simulation models based on temperature and concentration (Karaman et. al., 2012). The authors found that the effect of temperature on whistle phase parameters (for example, viscosity) could be successfully described by the Arrhenius relation. The authors also determined the activation energies for ketchup analyzed and described the effect of temperature and concentration on the activation energy (Karaman et. al., 2012; Sahin et. al., 2004; Bird, 1960). Some have used high-pressure microfluidization to improve the physical properties and lycopene content of ketchup products (Mert, 2012). Torbica et al. (Torbica et. al., 2016) evaluated the nutritional, rheological, and sensory properties of tomato ketchup with a high content of natural fibers obtained from grape fruit.
In the present work, we propose an original logarithmic expression correlating the shear stress and the square root of shear rate with only two adjustable parameters with some physical significance. The model is compared with some previous ones (Scott et. al., 1939; Reiner et. al., 1933; Ostwald , 1929; Herschel et. al., 1926; Tang et. al., 2004; Nagarani et. al., 2012; Mernone et. al., 2002; Ponalagusamy et. al., 2011; Chaturani et. al., 1982; Chaturani et. al., 1986; Hlaváč et. al., 2019; Vercet et. al., 2002; Herrmann et. al., 2013; Figura et. al.., 2007; Belda et. al., 2004; Heyes et. al., 1994).
Experimental part, Procedure (Materials and Methods of research)
The studied sample is a mixture, with the same mass composition, of about five different commercial textured tomato ketchup thickened with modified regular corn starch.
The mixing is realized using a blender-homogenizer (IKA Dispersers ULTRA-TURRAX ) at about 25 °C (1500 rpm and 15 min) for homogenization and to obtain a creamy and smooth texture.
The mixture was stored for 7 days to reach the equilibrium. Following this period, viscosity measurements were made. Rheological measurements were carried out with a Brookfield Digital DVII + rotary viscometer. Taking into account the experimental characteristics involved (cylindrical spindles of different standard sizes were used); shear rates of between 5.46 and 700.41 s-1 were employed to determine viscosity. The measurements of apparent viscosity were initially made with the non-agitated dispersions in increasing order of shear rate and a time intervals of 10 s, which enabled the corresponding up curve rheograms to be plotted. The temperature was maintained at 25 ± 0.5 °C throughout the measurement process by immersing the flasks in a thermostatic bath.
To reduce the temperature gradient between the Rheometer and the laboratory room for making the Rheometer thermostat block working at ease and giving more precision for the working fixed temperature, we maintained the temperature of the laboratory room also at 25°C using a split air-conditioner 24000 btu (Samsung Digital Inverter).
Results and Discussion
The results of the rheological properties of the studied tomato ketchup are summarized in Table 1. As shown in Table 1, the shear rate increases with the shear stress by analyzing the commercial ketchup. The relationship between rheological parameters for a non-Newtonian fluid is described principally by the following equation:
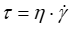 (1)
(1)
The values are in general an average of triplicate measurements; that is why some digits are written. We notice that our data behavior is roughly similar to those of the ketchup thickened with modified regular corn starch (symbolized by RSK) obtained in the literature under approximately similar conditions (Śmigielska et. al., 2013; Scott et. al., 1939).
The increase of shear stress (τ) and the decrease of apparent viscosity (η) versus the shear rate (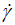 ) (Table 1, Figure 1), show that the tomato ketchup is a non-Newtonian complex fluid and it follows the behavior of the pseudoplastic or shear-thinning fluid (Reiner et. al., 1933; Ostwald, 1929).
) (Table 1, Figure 1), show that the tomato ketchup is a non-Newtonian complex fluid and it follows the behavior of the pseudoplastic or shear-thinning fluid (Reiner et. al., 1933; Ostwald, 1929).
In addition, the 3D-plot of the three rheological parameters (Figure 2), shear rates (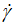 ), shear stress (τ), and apparent viscosity (η) gives an overview of monotonous mutual dependence. This global vision of the trends of scatter points and different types of curvature allows us to propose an adequate mathematical expression taking into account the different behaviors at very low and very high share rate (
), shear stress (τ), and apparent viscosity (η) gives an overview of monotonous mutual dependence. This global vision of the trends of scatter points and different types of curvature allows us to propose an adequate mathematical expression taking into account the different behaviors at very low and very high share rate (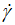 )-values, such as the power law and the parabolic branch in (
)-values, such as the power law and the parabolic branch in (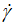 )-direction, respectively.
)-direction, respectively.
We notice that when the shear stress (τ) and the shear rate (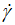 ) tend simultaneously to zero (Eq. 1), the ratio (τ/
) tend simultaneously to zero (Eq. 1), the ratio (τ/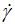 ) representing the apparent viscosity (η) has an indeterminate form in zero for which the lifting of the indetermination gives a non-zero limit value of the apparent viscosity of 13.00 Pa·s (Table 1). This operation required a nonlinear regression in a 9th degree polynomial with a correlation coefficient R greater than 0.99999, for which we have changed manually and slightly the obtained free value of the initial apparent viscosity until we observe the maximum of the correlation coefficient R. We have tested the limiting value of the derivative (∂τ/∂
) representing the apparent viscosity (η) has an indeterminate form in zero for which the lifting of the indetermination gives a non-zero limit value of the apparent viscosity of 13.00 Pa·s (Table 1). This operation required a nonlinear regression in a 9th degree polynomial with a correlation coefficient R greater than 0.99999, for which we have changed manually and slightly the obtained free value of the initial apparent viscosity until we observe the maximum of the correlation coefficient R. We have tested the limiting value of the derivative (∂τ/∂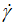 ) at zero of (
) at zero of (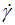 ) for confirming the obtained non-null limiting apparent viscosity.
) for confirming the obtained non-null limiting apparent viscosity.
Power low dependence and theoretical background
The most used model for complex fluids it the famous power law dedicated principally to the Ostwald-de Waele model (Bourne, 2002; Sahin et. al., 2004; Fortuna et. al., 2002), which is simply expressed as follows:
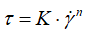 (2)
(2)
where K is the flow consistency index (SI units Pa·sn), is the shear rate or the velocity gradient perpendicular to the plane of shear (SI unit s−1), n is the flow behavior index (dimensionless), and τ is the shear stress (Pa).
We remember that the power-law fluids can be subdivided principally into three different types of non-Newtonian fluids based on the value of their flow (n) behavior index such as: pseudoplastic or shear-thinning (n<1), Newtonian fluid or shear-thickening fluids (n =1), and dilatants or shear-thickening (n<1),
The second used model (Eq. 3) is due to Herschel–Bulkley (Herschel et. al., 1926; Tang, et. al., 2004) in which the strain experienced by the fluid is related to the stress in a complicated, non-linear way.
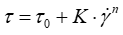 (3)
(3)
where is shear rate, K is the flow consistency index (SI units Pa·sn).
The third used model (Eq. 4) is due to the Casson model (Nagarani et. al., 2012; Mernone et. al., 2002; Ponalagusamy et. al., 2011; Chaturani et. al., 1982; Chaturani et. al., 1986; Hlaváč et. al., 2019) characterized by yield stress (τ0) and it has been widely used for modeling certain biological fluids.
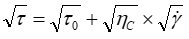 (4)
(4)
where τ0 is yield stress and ηC the Casson plastic viscosity. We note that the Eq. 4 is valid for (τ ≥ τ0) and we must consider = 0 when τ ≤ τ0.
Modeling Methodology
Due to the great varieties of rheological fluids and its very different behaviors for which some existing models succeed more than others due to some specific features for each studied complex fluid, we suggest an original empirical equation with logarithm and power mathematical form (Eq. 5). In fact, regarding the power behavior of the shear stress (τ) of the tomato ketchup against the shear rate (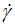 ) with a flow behavior index (n) less than unit due to the pseudoplastic (shear thinning) behavior, we propose an original empirical two parameters-equation esteeming the abovementioned characteristics with a global form expressed as follows:
) with a flow behavior index (n) less than unit due to the pseudoplastic (shear thinning) behavior, we propose an original empirical two parameters-equation esteeming the abovementioned characteristics with a global form expressed as follows:
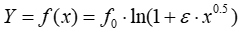 (5)
(5)
where f0 and ε are two free adjustable parameters, and x and Y represent the shear rate ( ) and the shear stress (τ) respectively.
In fact, at high shear rate values (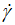 ) the plot of the logarithm form exhibits a parabolic branch and the variation can describe eventual yield stress characterizing the studied pseudoplastic sauce. On the other hand, at very low shear rate values (
) the plot of the logarithm form exhibits a parabolic branch and the variation can describe eventual yield stress characterizing the studied pseudoplastic sauce. On the other hand, at very low shear rate values (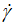 ), the asymptotic expansion of the expression (Eq. 5) gives a dominant term (x0.5) expressed as follows:
), the asymptotic expansion of the expression (Eq. 5) gives a dominant term (x0.5) expressed as follows:
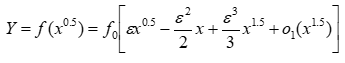 (6)
(6)
Then the common factorization leads to the following simplified equation:
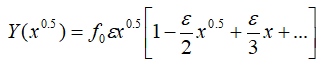 (7)
(7)
For which this obtained expression shows principally a power-dependence (n0=0.5) and the polynomial in square brackets adjusts (or corrects) somewhat the true power-dependence (with an increment δn) of the studied rheological system, and gives then a global power (n=0.5±δn) correcting well like the (Eqs. 2-4), the variation of the shear stress (τ) vs. the shear rate values (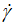 ) around zero for the studied sauce.
) around zero for the studied sauce.
Moreover, similarly to the existing power laws (Eqs. 2-4), which exhibit a divergence of the derivative of (τ) vs. (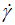 ) characterized by quasi-vertical asymptote at very low shear rate values (
) characterized by quasi-vertical asymptote at very low shear rate values (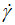 ) values, the suggested model satisfies also this property where the asymptote expansion can be expressed around
) values, the suggested model satisfies also this property where the asymptote expansion can be expressed around ≈0+ as follows:
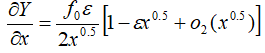 (8)
(8)
where the (x0.5)-term in the denominator is responsible for the observed divergence.
In addition, taking into account the dimensional analysis on physical quantities described in Eq. 5, we have tried to upgrade the proposed equation to a semi-empirical model by giving explicit sense and physical meaning of each adjustable parameter. So, Eq. 5 can be re-expressed as follows:
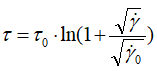 (9)
(9)
Where τ0 represents somewhat yield stress or critical shear stress, and represents a critical shear rate and can be close to the equivalent reciprocal flow consistency index related to the power-law (Eq. 2), for which we can define an extra parameter such as a critical apparent viscosity (η0) expressed as follows:
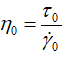 (10)
(10)
In the experimental section, we have chosen to test the suggested model on a blended and homogenized mixture of five different commercial textured tomato ketchups thickened with modified regular corn starch in order to obtain average values of obtained optimal free adjustable parameters, which can be considered as a certain reference for future discussion and interpretation on new parameters values of individually studied ketchup or why not for any other pseudoplastic plastic systems.
So, for future application and assessment of the present suggested model on other individual tomato ketchup systems (Vercet et. al., 2002; Herrmann et. al., 2013; Figura et. al.., 2007; Belda et. al., 2004; Heyes et. al., 1994), the different obtained parameters’ values can give a specific discussion, criterion on each feature of the studied system especially when the other ones are fixed. We can cite, for example, the comparison of parameters’ values between studied sauces derived from different botanical origins used different thickeners such as corn, potato, maize, waxy maize starches, etc. Moreover, the effect on the parameters values of the added ingredients, pH, texture, etc. can be an interesting subject of discussion and interpretation of the amount of obtained parameters.
Model application and comparison
Table 2 represents the results of the fitting using the non-linear regression method for the suggested models and the three-abovementioned ones. In the same way, Figure 3 shows the variation of the experimental and the four different calculated shear stresses (τ) versus shear rate (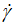 ).
).
Regarding the values of the standard deviation (SD) and standard error (SE), we can conclude that our model is reliable and well describes the variation of the shear stresses (τ) versus shear rate (
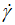 ).
).
In the same context, Table 3 summarized the obtained parameters values of different models. We note that our results are close to those of the ketchup thickened with modified regular corn starch (symbolized by RSK) obtained in the literature under the same conditions [4, 36].
Mathematical analysis of the model
Starting from our suggested model (Eq. 9) containing a half-power dependence into the argument of logarithm and expressed by the square root of shear rate ( ), we have thought to test another power (n) other than 0.5. So, we have rewritten the suggested model to a new power form expressed by Eq. 11.
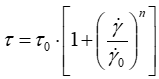 (11)
(11)
In a new fitting in non-linear regression, when we take both the three parameters (τ0,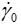 ,n) as free adjustable parameters in the fitting with non-linear regression, we observe that there are infinite possible optimal solutions and the software’s iterations move to the sense of the decrease of n-values and the increase of (τ0,
,n) as free adjustable parameters in the fitting with non-linear regression, we observe that there are infinite possible optimal solutions and the software’s iterations move to the sense of the decrease of n-values and the increase of (τ0, 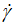 0) for each round of iteration.
0) for each round of iteration.
Nevertheless, when the 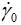 -parameter is fixed with high values (from 103 to 1015 or more), we observe that the discrepancy is satisfactorily reduced and the power (n) tends to a limiting value about nlim ≈ 0.3295 (Figure 4). We can then use this option to obtaining a very satisfactory agreement but with a very high couple values of (τ0,
-parameter is fixed with high values (from 103 to 1015 or more), we observe that the discrepancy is satisfactorily reduced and the power (n) tends to a limiting value about nlim ≈ 0.3295 (Figure 4). We can then use this option to obtaining a very satisfactory agreement but with a very high couple values of (τ0,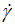 0), which are devoid of any physical significance. The statistical parameters values become about (SD≈1.578, SE≈0.298), which are best compared with those of Table 3 for fixed n = 0.5. Nevertheless, we note that these values of SD and SE are identical to those of the Ostwald-de Waele model (Table 3, Eq. 2).
0), which are devoid of any physical significance. The statistical parameters values become about (SD≈1.578, SE≈0.298), which are best compared with those of Table 3 for fixed n = 0.5. Nevertheless, we note that these values of SD and SE are identical to those of the Ostwald-de Waele model (Table 3, Eq. 2).
Considering the very high values of (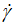 0) compared to those of experimental shear rate (
0) compared to those of experimental shear rate (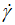 ) given in Table 3, we can consider that the ratio (
) given in Table 3, we can consider that the ratio (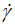 /
/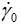 ) is very low and the expression of Eq. 11 can be written in an asymptotic expansion expressed as follows:
) is very low and the expression of Eq. 11 can be written in an asymptotic expansion expressed as follows:
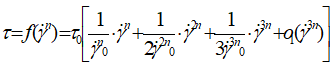 (12)
(12)
And the common factorization leads to the following simplified equation:
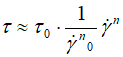 (13)
(13)
This clearly joins the expression of the Ostwald-de Waele model (Eq. 2). That is why we found the same value of (n=0.3295) in Table 3 and we can see easily the equality between the K-value of Eq. 2 and (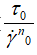 )-value of Eq. 13 which is equal to 19.50 (Table 3).
)-value of Eq. 13 which is equal to 19.50 (Table 3).
Regarding these complications on the flow behavior index (n) for different models, we saw good to think about the real flow behavior index ν(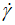 ), which depends on each value of (
), which depends on each value of (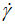 ) reflecting then the shear behavior for each shear rate value. Then, we can call it the current shear rate (ν), which can be calculated through the derived function defined by Eq. 14 and deduced from the transformed derivative of the Ostwald-de Waele power-law expression (Eq. 2).
) reflecting then the shear behavior for each shear rate value. Then, we can call it the current shear rate (ν), which can be calculated through the derived function defined by Eq. 14 and deduced from the transformed derivative of the Ostwald-de Waele power-law expression (Eq. 2).
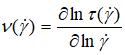 (14)
(14)
If we suppose that the rheological behavior follows our suggested model (Eq. 9), the current shear rate (ν) can be calculated using the following expression:
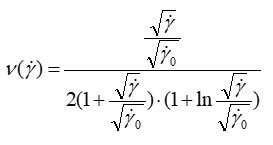
(15)
Mathematically, we can see that it is about a descending function starting from 0.5, which is confirmed by the asymptotic expansion of Eq. 7 and tending slowly to zero at infinity.
Experimentally, the plot of the curve representing ln(τ) as a function of ln(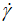 ) for the studied commercial textured tomato ketchup is shown by (Figure 5). We observe a quasi-linear dependence at high values of shear stress (
) for the studied commercial textured tomato ketchup is shown by (Figure 5). We observe a quasi-linear dependence at high values of shear stress (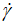 ) showing normal power dependence very close to the Herschel–Bulkley model (Eq. 3), while at low values of shear stress (
) showing normal power dependence very close to the Herschel–Bulkley model (Eq. 3), while at low values of shear stress (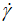 ) the rheological behavior is somewhat complicated by some change of curvatures.
) the rheological behavior is somewhat complicated by some change of curvatures.
Nevertheless, for the experimental data representation, the complicated curvature in the low shear rate region and the lack of precision and experimental data number necessitates using fittings to a high polynomial degree. So, remedying to this inconvenience, we can also simply determinate otherwise the values of the current shear rate (ν) by fitting the plot of the curve (Figure 6) representing the natural logarithm of the experimental apparent viscosity ln(η) against the natural logarithm of the shear rate ln(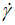 ) in polynomial non-linear regression. Due to the double dependence (Eq. 1) of (η) on (τ) and (
) in polynomial non-linear regression. Due to the double dependence (Eq. 1) of (η) on (τ) and (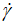 ), the apparent viscosity becomes an endogen variable and gives more simplified and low curvature (Figure 6) at low values of shear stress (
), the apparent viscosity becomes an endogen variable and gives more simplified and low curvature (Figure 6) at low values of shear stress (
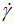 ) permitting then an optimal fitting with less degree polynomial.
) permitting then an optimal fitting with less degree polynomial.
Otherwise, the current shear rate (ν) by the following equation:
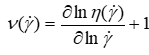 (16)
(16)
So, the derivation of the natural logarithm of the experimental apparent viscosity ln(η) against the natural logarithm of the shear rate ln(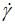 ) represented by Figure 6 gives interesting results on the variation of the experimental and calculated (Eq. 9) current shear rate (ν) with the shear rate (
) represented by Figure 6 gives interesting results on the variation of the experimental and calculated (Eq. 9) current shear rate (ν) with the shear rate (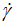 ). Figure 7 shows that experimental values of ν decrease from 1 confirming then the abovementioned non-zero limit value of the apparent viscosity (13 Pa·s) while the calculated ones decrease from 0.5 which is predicted by the asymptotic expansion of Eq. 7. The spectacular finding is that the experimental current shear rate exhibits a curious minimum of about 0.2731 at a low shear rate (
). Figure 7 shows that experimental values of ν decrease from 1 confirming then the abovementioned non-zero limit value of the apparent viscosity (13 Pa·s) while the calculated ones decrease from 0.5 which is predicted by the asymptotic expansion of Eq. 7. The spectacular finding is that the experimental current shear rate exhibits a curious minimum of about 0.2731 at a low shear rate (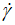 ≈30s-1) and then increases to reaching a pseudo-plateau with a limiting value of about 0.3553 and it continues to increase very slightly with a negligible variation. We note that this new finding of the variations of the current shear rate (ν) can open new interesting theoretical researches to explain what happens as structural changes or rheological phenomena in molecular layers, shear plans, etc.
≈30s-1) and then increases to reaching a pseudo-plateau with a limiting value of about 0.3553 and it continues to increase very slightly with a negligible variation. We note that this new finding of the variations of the current shear rate (ν) can open new interesting theoretical researches to explain what happens as structural changes or rheological phenomena in molecular layers, shear plans, etc.
We conclude that our suggested model (Eq. 9) has the advantage to give a variable current shear rate (ν) against the shear rate ( ) while the Ostwald-de Waele (Eq. 2) and Herschel–Bulkley (Eq. 3) models give a global constant shear rate (n). For this purpose, we think about the value of the experimental global shear rate (ng,exp), as well as the calculated global one related to the suggested model (ng,cal). So, we must calculate the average value of the (
) while the Ostwald-de Waele (Eq. 2) and Herschel–Bulkley (Eq. 3) models give a global constant shear rate (n). For this purpose, we think about the value of the experimental global shear rate (ng,exp), as well as the calculated global one related to the suggested model (ng,cal). So, we must calculate the average value of the (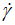 )-function over the interval of [0,700.41] using the integral expressed as follows:
)-function over the interval of [0,700.41] using the integral expressed as follows:
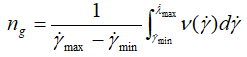 (17)
(17)
where min =0,
max=700.41, and ν(γ) should be expressed by a well-chosen polynomial with an optimal degree or directly calculated by the software. For our case, we found the experimental global shear rate (ng,exp) equal to 0.3441 and the calculated global one (ng,cal) equal to 0.3126. Consequently, we see that the two obtained values are near that of Ostwald-de Waele (n=0.3295), which shows a good agreement with the experimental data (Figure 3). Note, regarding the variation of the new concept of current shear rate (ν) against the shear rate (
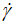 ), the experimental global shear rate (ng,exp) is strongly affected by the studied shear rate range.
), the experimental global shear rate (ng,exp) is strongly affected by the studied shear rate range.
Conclusion
We have suggested a new equation correlating the shear stress (τ) against the shear rate (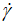 ) for the studied commercial textured tomato ketchup thickened with modified regular corn starch. The proposed expression has two mathematical characteristics, such as (a): the logarithm function has a non-exponential parabolic branch, i.e., for the large values of the shear rate (
) for the studied commercial textured tomato ketchup thickened with modified regular corn starch. The proposed expression has two mathematical characteristics, such as (a): the logarithm function has a non-exponential parabolic branch, i.e., for the large values of the shear rate (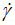 ), which fits well with the variation of the experimental values of shear stress (τ). (b): the square-rooted term of the shear rate (
), which fits well with the variation of the experimental values of shear stress (τ). (b): the square-rooted term of the shear rate (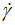 ) into the logarithmic argument has the property of the power trend in the region of very low values of the shear rate (
) into the logarithmic argument has the property of the power trend in the region of very low values of the shear rate (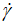 ), (i.e. the mathematical function has an asymptotic expansion in power-law against the shear rate (
), (i.e. the mathematical function has an asymptotic expansion in power-law against the shear rate (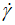 ), which is a good framework for the behavior of the shear stress (τ) for the case of ketchup in very feeble values of shear rate (
), which is a good framework for the behavior of the shear stress (τ) for the case of ketchup in very feeble values of shear rate (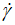 ). In addition, we have given physical significance for the adjusted parameters of the proposed empirical equation.
). In addition, we have given physical significance for the adjusted parameters of the proposed empirical equation.
We conclude that this model is in good agreement with experimental data and has approximately the same quality or better than the previous models of the literature.
Regarding that, the ketchup has a pseudoplastic (thinning) rheological behavior; we notice that this model can be tested for other non-Newtonian fluids having the same rheological properties (Vercet et. al., 2002; Herrmann et. al., 2013; Figura et. al.., 2007; Belda et. al., 2004; Heyes et. al., 1994).
Disclosure statement
No potential conflict of interest was reported by the authors.
References
Alexandrovich, S. O., Yurievna, V. S., Olegovich, P. I., Yurievna, K. N., Ilyinichna, V. L., & Pavlovna, Y. T. (2018). Provision of Microbiological Safety in The Food Industry Based on Special Technological Supporting Solutions. International Journal of Pharmaceutical Research & Allied Sciences, 7(1), 103-13.
Bayod, E., Willers, E. P., Tornberg, E. (2008). Rheological and structural characterization of tomato paste and its influence on the quality of ketchup. LWT - Food Sci. Techn., 41(7), 1289–1300.
Belda, B., Herraez, J. V., Diez, O. (2004). Rheological study and thermodynamic analysis of the binary system (water/ethanol): Influence of concentration. Phys. Chem. Liq., 42(5), 467–479.
Bikić, S., Bukurov, M., Babić, M., Pavkov, I., Radojčin, M. (2012). Rheological behavior of quince (Cydonia oblonga) puree. J. Process. Energy Agr. , 16(4), 155 –161.
Bird, R. B, Stewart, W. E., Lihgtfoot, E. N. (1960). Transport Phenomena., John Wilie & Sons., New York.
Bourne, M. C. (2002). Food Texture and Viscosity. Concept and Measurement. Academic Press, London.
Božiková, M., Hlaváč, P., (2010). Selected physical properties of agricultural and food products – Scientific Monograph, SUA in Nitra, 178 p. Bukurov.
Bukurov, M., Bikić, S., Babić, M., Pavkov, I. (2012). Radojčin M. Rheological behavior of Senga Sengana strawberry mash. J. Process. Energy Agr., 16(4), 142 –146.
Chaturani, P., Ponnalagarsamy, R. (1982). A two layered model for blood flow through stenosed arteries. Proceedings of the 11th National Conference on Fluid Mechanics and Fluid Power, 16–22.
Chaturani, P., Samy, R. P. (1986). Pulsatile flow of Casson's fluid through stenosed arteries with applications to blood flow. Biorheology., 23(5), 499–511.
Diósi, G., Móré, M., Sipos, P. (2014). Rheological properties of the mixture product of apple pomace and wheat flour. J. Process. Energy Agr., 18(4), 151 –153.
Dizayee, A. S., & Maaroof, S. M. (2019). Growth analysis of intercropped Wheat, Chickpea and wild Mustard based on physical and thermal time scales. Journal of Advanced Pharmacy Education & Research| Apr-Jun, 9(2), 108-114.
Fakhrabad, M. S., & Abedi, B. (2019). Investigation of the Effect of Foliar Application of Seaweed Extract as growth bio-stimulants (Ascophyllum nodosum) on Quantitative and Qualitative Characteristics of Three Tomato Cultivars (Solanum Lycopersicon Mill). World Journal of Environmental Biosciences, 8(4), 19-22.
Figura, L. O., Teixeira, A. A. (2007). Food Physics, Physical properties – measurement and applications (1st ed.), Verlag, Berlin, Heidelberg, New York: Springer.
Fortuna, T., Juszczak, L., (2002). Stachura M. Influence of acetylated distarch adipate on some rheological properties of ketchup. Pol. J. Food Nutr. Sci., 3(11/52), 39–43.
Glicerina, V., Balestra, F., Dalla Rosa, M., Romani, S. (2013). The influence of process steps on microstructural, rheological and thermal properties of dark chocolate. J. Process. Energy Agr., 17(2), 59 – 63.
Hailu, F. A., Wakjira, M., & Getahun, A. (2018). Fishpond Wastewater Versus Chemical Fertilizer On Tomato Productivity In Jimma, Oromia Region, Ethiopia. World Journal of Environmental Biosciences, 7(4), 82-89.
Herrmann, J., Alayón, A. B., Trembley, J., Grupa, U. (2013). Development of a rheological prediction model for food suspensions and emulsions. Int. J. Food Eng., 115(4), 481–485.
Herschel, W. H., Bulkley, R. (1926). Konsistenzmessungen von Gummi-Benzollösungen. Kolloid Zeitschrift, 39(4), 291–300.
Heyes, D. M., March, N. H. (1994). Mechanical Properties of Liquids: Newtonian and Beyond. Phys. Chem. Liq., 28(1), 1–27.
Hlaváč, P., Božiková, M. (2012). Influence of temperature and storing time on flower honey rheologic and thermophysical properties. J. Process. Energy Agr., 16(2), 52 –56.
Hlaváč, P., Božiková, M., Petrović, A., Ardonová, V., Kotoulek, P. (2019). Temperature and storing time effect on rheologic properties of selected tomato ketchups, J. Process. Energy Agr., 23(2), 78–82.
Karaman, S., Yilmaz, M. T., Cankurt, H., Kayacier, A., Sagdic, O. (2012). Linear creep and recovery analysis of ketchup–processed cheese mixtures using mechanical simulation models as a function of temperature and concentration. Food Res. Int., 48(2), 507–519.
Kubík, Ľ., Brindza, J., Brovarskyi, V., Velychko, S. (2017). Perga under compressive loading. J. Process. Energy Agr. 21(1), 23 –26.
Kubík, Ľ., Doležajová, M., (2014). Determination of mechanical properties of greengage plum Prunus Angeleno, J. Process. Energy Agr., 18(1), 14 –17.
Liu, F., Cao, X., Wang, H., Liao, X. (2010). Changes of tomato powder qualities during storage. Powder Technol., 204(1), 159 –166.
Mernone, A. V., Mazumdar, J. N., Lucas, S. K. (2002). A mathematical study of peristaltic transport of a Casson fluid. Math. Comp. Mod., 35(7-8), 895–912.
Mert, B. (2012) Using high pressure microfluidization to improve physical properties and lycopene content of ketchup type products. Food Bioprod. Process., 109(3), 579–587.
Micić, D., Ostojić, S., Simonović. M., Simonović, B. R. (2014). Thermal behavior of raspberry and blackberry seeds oils followed by DSC. J. Process. Energy Agr. , 18(5), 204 –206.
Nagarani, P., Lewis, A. (2012). Peristaltic flow of a Casson fluid in an annulus. Korea Australia Rheology J., 24(1), 1–9.
Ostwald, W. (1929). Ueber die rechnerische Darstellung des Strukturgebietes der Viskosität. Kolloid Zeitschrift, 47(2), 176–187.
Ponalagusamy, R., Tamil Selvi, R. (2011). A study on two-layered model (Casson-Newtonian) for blood flow through an arterial stenosis: axially variable slip velocity at the wall. J. Franklin Inst. Eng. Appl. Math., 348(9), 2308–2321.
Reiner, M., Schoenfeld-Reiner, R. (1933). Viskosimetrische Untersuchungen an Lösungen hochmolekularer Naturstoffe. I. Mitteilung. Kautschuk in Toluol. Kolloid Zeitschrift , 65(1), 44-62.
Ruiz Celma, A., Cuadros, F., López-Rodríguez, F. (2009). Characterisation of industrial tomato by-products from infrared drying process. Food Bioprod. Process., 87(4), 282–291.
Sahin, H., Ozdemir, F. (2004). Effect of some hydrocolloids on the rheological properties of different formulated ketchups. Food Hydrocolloids, 18(6), 1015–1022.
Scott Blair, G. W., Hening, J. C., Wagstaff, A. (1939) The Flow of Cream through Narrow Glass Tubes. J. Phys. Chem., 43(7), 853–864.
Sharoba, A. M., Senge, B., El-Mansy, H. A., Bahlol, H. E. I. M. (2005). Blochwitz R. Chemical, sensory and rheological properties of some commercial German and Egyptian tomato ketchups. Europ. Food Res. Techn. , 220(2), 142–151
Śmigielska, H., Lewandowicz, J., Thanh-Blicharz, J. L., (2013). Effect of type 4 resistant starch on colour and rheological properties of tomato ketchup (in Polish). Żywność. Nauka. Technologia. Jakość, 2(87), 137 –149.
Tan, J., Kerr, W. L. (2015). Rheological properties and microstructure of tomato puree subject to continuous high pressure homogenization. Food Bioprod. Process., 166, 45–54.
Tang, H. S., Kalyon, D. M. (2004). Estimation of the parameters of Herschel–Bulkley fluid under wall slip using a combination of capillary and squeeze flow viscometers. Rheologica Acta, 43(1), 80–88.
Torbica, A., Belović, M., Mastilović, J., Kevrešan, Ž., Pestorić, M., Škrobot, D., Dapčević, Hadnađev, T. (2016) Nutritional, rheological, and sensory evaluation of tomato ketchup with increased content of natural fibres made from fresh tomato pomace. Food Bioprod. Process. , 98, 299 –309.
Vercet, A., Sánchez, C., Burgos, J., Montañés, L., Buesa, P. L. (2002). The effects of manothermosonication on tomato pectic enzymes and tomato paste rheological properties. Int. J. Food Eng., 53(3), 273–278.
Yilmaz, M. T., Karaman, S., Cankurt, H., Kayacier, A., Sagdic, O. (2011). Steady and dynamic oscillatory shear rheological properties of ketchup–processed cheese mixtures: Effect of temperature and concentration. J. Food Eng., 103(2), 197–210.
Zhang, L., Schultz, M. A., Cash, R., Barrett, D. M,, McCarthy, M. J. (2014). Determination of quality parameters of tomato paste using guided microwave spectroscopy. Food Control, 40, 214–223.
Table 1. Experimental values of the shear stress (τ) and the apparent viscosity (η) for different shear rates ( ) of the analyzed commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure.
|
|
τexp |
ηexp |
|
s-1 |
Pa |
Pa·s |
|
0.0000 |
0.0000 |
13.000a |
|
5.4582 |
34.433 |
6.3085 |
|
13.648 |
50.194 |
3.6778 |
|
20.922 |
56.671 |
2.7087 |
|
37.292 |
65.901 |
1.7672 |
|
52.761 |
71.302 |
1.3514 |
|
67.309 |
76.682 |
1.1392 |
|
83.138 |
82.070 |
0.98715 |
|
100.06 |
87.456 |
0.87406 |
|
120.07 |
93.607 |
0.77960 |
|
146.44 |
100.64 |
0.68720 |
|
171.92 |
105.16 |
0.61168 |
|
200.12 |
110.54 |
0.55240 |
|
229.22 |
115.94 |
0.50578 |
|
261.97 |
120.57 |
0.46025 |
|
300.17 |
125.96 |
0.41963 |
|
333.83 |
130.68 |
0.39146 |
|
372.04 |
135.22 |
0.36347 |
|
400.23 |
139.07 |
0.34748 |
|
430.25 |
142.92 |
0.33218 |
|
468.45 |
146.78 |
0.31333 |
|
500.29 |
150.64 |
0.30110 |
|
507.56 |
151.19 |
0.29786 |
|
536.67 |
154.49 |
0.28787 |
|
573.97 |
159.10 |
0.27719 |
|
600.35 |
162.18 |
0.27014 |
|
650.38 |
166.21 |
0.25555 |
|
700.41 |
170.93 |
0.24404 |
a: extrapolated value using non-linear regression of 9th-degree polynomial with R> 0.99999.
Table 2. Comparison between experimental and calculated values of the shear stress (τ) or different shear rates ( ) of the analyzed commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. τcal (Eq. 9), τOstwald (Eq. 2), τHerschel (Eq. 3), τCasson (Eq. 4), and the corresponding standard deviation (SD) and standard error (SE).
|
|
τexp |
τcal |
τOstwald |
τHerschel |
τCasson |
|
s-1 |
Pa |
||||
|
0.0000 |
0.000 |
0.000 |
0.000 |
2.0220 |
46.933 |
|
5.4582 |
34.433 |
27.594 |
34.0228 |
37.833 |
55.042 |
|
13.648 |
50.194 |
41.170 |
46.0174 |
48.148 |
60.053 |
|
20.922 |
56.671 |
49.222 |
52.9733 |
54.332 |
63.416 |
|
37.292 |
65.901 |
62.097 |
64.0868 |
64.470 |
69.492 |
|
52.761 |
71.302 |
70.989 |
71.8497 |
71.718 |
74.264 |
|
67.309 |
76.682 |
77.770 |
77.8527 |
77.407 |
78.259 |
|
83.138 |
82.070 |
84.016 |
83.4639 |
82.786 |
82.241 |
|
100.06 |
87.456 |
89.776 |
88.7179 |
87.875 |
86.192 |
|
120.07 |
93.607 |
95.699 |
94.2106 |
93.244 |
90.558 |
|
146.44 |
100.64 |
102.435 |
100.580 |
99.531 |
95.929 |
|
171.92 |
105.16 |
108.095 |
106.040 |
104.97 |
100.81 |
|
200.12 |
110.54 |
113.629 |
111.482 |
110.43 |
105.92 |
|
229.22 |
115.94 |
118.718 |
116.582 |
115.59 |
110.96 |
|
261.97 |
120.57 |
123.854 |
121.827 |
120.93 |
116.38 |
|
300.17 |
125.96 |
129.217 |
127.416 |
126.66 |
122.44 |
|
333.83 |
130.68 |
133.495 |
131.957 |
131.35 |
127.58 |
|
372.04 |
135.22 |
137.936 |
136.754 |
136.32 |
133.23 |
|
400.23 |
139.07 |
140.973 |
140.085 |
139.80 |
137.29 |
|
430.25 |
142.92 |
144.016 |
143.464 |
143.33 |
141.52 |
|
468.45 |
146.78 |
147.637 |
147.542 |
147.61 |
146.79 |
|
500.29 |
150.64 |
150.469 |
150.774 |
151.02 |
151.08 |
|
507.56 |
151.19 |
151.094 |
151.492 |
151.78 |
152.05 |
|
536.67 |
154.49 |
153.522 |
154.302 |
154.75 |
155.90 |
|
573.97 |
159.10 |
156.473 |
157.756 |
158.42 |
160.74 |
|
600.35 |
162.18 |
158.462 |
160.110 |
160.92 |
164.12 |
|
650.38 |
166.21 |
162.035 |
164.389 |
165.49 |
170.41 |
|
700.41 |
170.93 |
165.378 |
168.453 |
169.85 |
176.58 |
|
|
SD / Pa |
2.945 |
1.578 |
1.146 |
10.232 |
|
|
SE / Pa |
0.577 |
0.298 |
0.221 |
1.934 |
Table 3. Values of rheological model parameters used to describe flow curves of analyzed commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. Ostwald-de Waele (Eq. 2), Herschel–Bulkley (Eq. 3), Casson (Eq. 4), suggested model (Eq. 9), and corresponding standard deviation (SD) and standard error (SE).
|
Model |
τ0 |
K |
n |
γ0 |
η0 |
SD |
SE |
|
Pa |
Pa·sn |
- |
s-1 |
Pa·s |
Pa |
Pa |
|
|
Ostwald-de Waele |
- |
19.449 ±0.384 |
0.3295 ±0.0034 |
- |
- |
1.578 |
0.298 |
|
Herschel–Bulkley |
13.103 ±0.491 |
12.968 ±0.123 |
0.3804 ±0.0008 |
- |
- |
1.146 |
0.221 |
|
Casson |
46.933 ±1.468 |
|
0.5 ±0.0 a |
793.189 b ±61.406 |
0.05917 ±0.00273 |
10.232 |
1.934 |
|
Suggested model |
122.229 ±7.406 |
- |
0.5 ±0.0 a |
85.089 ±16.972 |
1.4365b ±0.3736 |
2.945 |
0.577 |
|
3.544×107 ±4.67×106 |
- |
0.3295 ±0.0036 |
1019 ±0.0 a |
3.54×10-12b ±4.7×10-13 |
1.578 |
0.298 |
a: Fixed parameter in the fit; b: extra parameter calculated from Eq. 1.
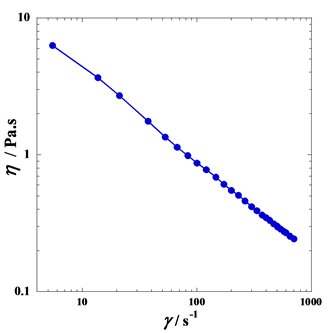
Figure 1. Variation of the apparent viscosity (η) versus shear rate ), in double logarithm scale, for five blended commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure.
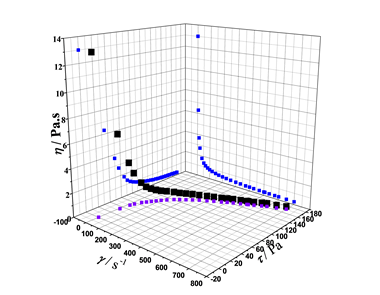
Figure 2. 3D-plot of the three coupled rheological parameters of Eq. 1 describing the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure.
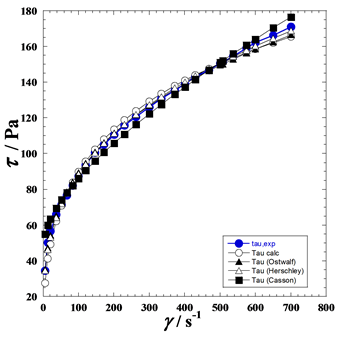
Figure 3. Variation of the shear stress (τ) versus shear rate () for five blended commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. (●): Experimental; (○): suggested model (Eq. 9); (▲): Ostwald-de Waele (Eq. 2); (∆): Herschel–Bulkley (Eq. 3), and (■): Casson (Eq. 4),
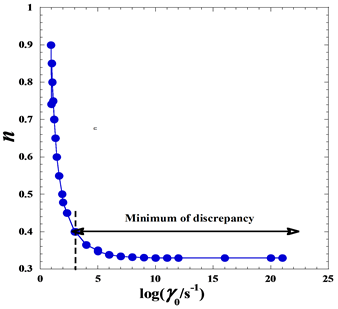
Figure 4. Variation of the pseudo flow behavior index (n) of Eq. 11 with the decimal logarithm of critical shear rate log(γ0) defined in Eq. 9, for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure.
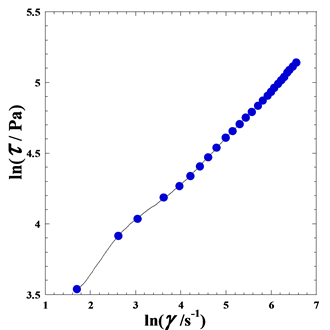
Figure 5. Variation of the natural logarithm of the experimental shear stress ln(τ) against the natural logarithm of the shear rate ln(γ) for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure.
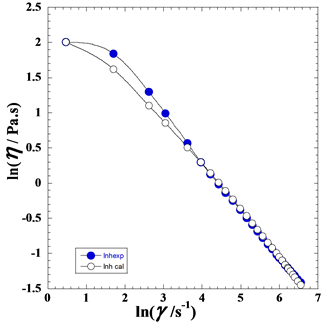
Figure 6. Variation of the natural logarithm of the experimental apparent viscosity ln(η) against the natural logarithm of the shear rate ln(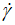 ) for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. (●): Experimental; (○): Calculated by the suggested model (Eq. 9);
) for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. (●): Experimental; (○): Calculated by the suggested model (Eq. 9);
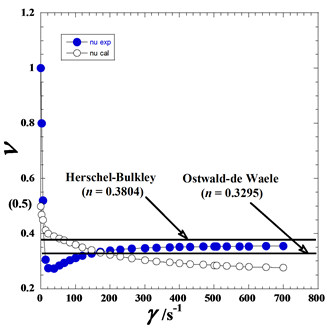
Figure 7. Variation of current shear stress (ν) against the shear rae (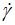 ) for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. (●): Experimental; (○): Calculated by fitting of ln(η) vs. ln(γ) of the suggested model (Eq. 9).
) for the studied commercial textured tomato ketchup thickened with modified regular corn starch at room temperature and atmospheric pressure. (●): Experimental; (○): Calculated by fitting of ln(η) vs. ln(γ) of the suggested model (Eq. 9).